Easily compare shell shapes and hypothetical mobility
Ammonoids are most closely related to octopus, squid, and cuttlefish, which each have different capacities for swimming. Shells limited the ability of ammonoids to move through the ocean waters. Some shells were more streamlined that others. What aspects of shell shape matter for hydrodynamics?
Umbilical Exposure
When previous shell coils are exposed, they cause turbulence.
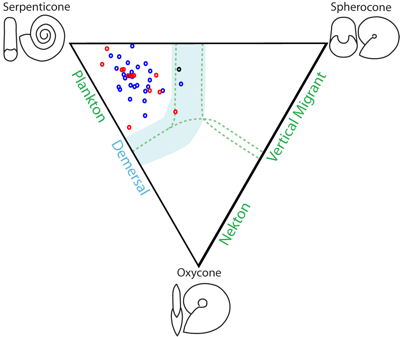
Hydrodynamic experiments suggest the shell shapes of certain ammonoids were suited to different speeds and modes of locomotion.
Left: earliest Jurassic Psiloceras shells collected by Guex (1995) in Nevada are serpenticonic, and may have had drifting life modes.
It doesn’t take long to plot data from any planispiral ammonoid shell collection in Westermann Morphospace with any spreadsheet or graphing language. Download the program in R below or email Kathleen: ritterbush@uchicago.edu
Download:
Stability, buoyancy, and position are all important, but these particular shape aspects heavily influence drag:
Could Ammonoids Swim?
Whorl Expansion
When the body chamber expands greatly as the shell builds a coil, balance and streamlining typically improve.
Overall Inflation
Narrow forms present a reduced profile to drag forces at the front of the shell, and are more efficient at high speeds or large sizes.
contact: Kathleen at ritterbush@uchicago.edu
Shell Measurements
Shape Parameters
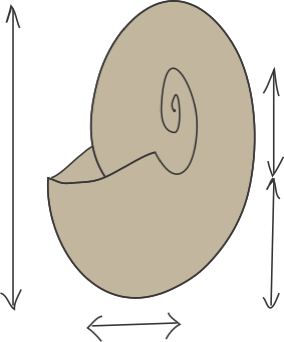
Diameter
Umbilical Diameter
Whorl Aperture (a)
remainder is a’
Shell Thickness (b)
Measure this using a separate photograph, taken from the side.
Umbilical Exposure
U = Umbilical Diameter / Diameter
Whorl Expansion
w = a / a’
Thickness Ratio
Th = b / Diameter
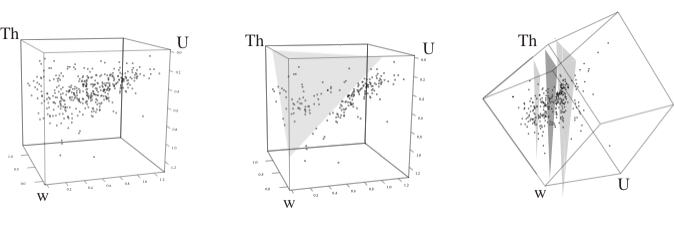
Westermann Morphospace Projection
Data for all three parameters can be projected into a 3d space. The axes can be squeezed and scaled without changing the relative positions of data points.
The data are projected onto a ternary diagram, which is effectively a triangle over the origin in 3d space.
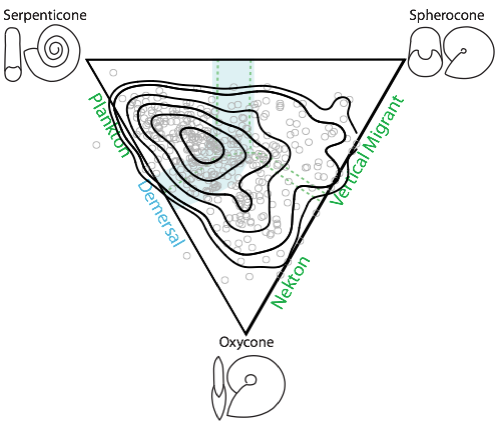
Based on data from Jacobs, 1992 variation in drag significantly correlates with data orientation to the Westermann Morphospace projection plane. These illustrated triangles (left) would eclipse together when viewed in Westermann Morphospace.
Density contours over 402 specimens from Raup (1967).