Forced Rossby Waves

When the time scale of the flow is much longer than the rotation time scale of the apparatus (i.e., Ro <<1), the flow tends to become layerwise 2D (Taylor-Proudman theorem). As such, it can be described in terms of streamfunction. In this limit, (the vertical component of) relative vorticity is equal to the curvature of streamfunction. Therefore, a meandering flow is characterized by a train of positive and negative vorticities. Here, we will demonstrate how a meandering wave pattern is created by a flow impinging on an obstacle at the bottom.

The following movie shows the flow pattern in a rotating annulus, visualized by red dye. The annulus partially filled with water (~ 7 cm deep) is spun up counterclockwise to 2.7 radians per second and allowed to settle into a rigid body rotation. There is a narrow ridge at the bottom across the annulus at certain "longititude." Notice that the free surface is shaped into a parabola due to centrifugal force, so there is a significant depth difference between the inner and outer walls of the annulus (see below). As we will see, this is crucial for the generation of waves.

After injecting dye near the inner wall of the annulus and letting it sit for a while (ignore the small vortices at the boundary of the dye), we reduce the rotation of the turntable to 2.4 rad/sec. Due to inertia, this creates a prograde (counterclockwise) flow in the azimuthal direction (0.3 rad/sec). As the flow passes over the ridge, the dye develops a meandering pattern downstream, and more wave crests are created further downstream as time goes on.

The diagram below illustrates the behavior of the vortex tube following the trajectory of the fluid. The tube in the upstream of the ridge has the length h₀ and zero relative vorticity (but 2Ω background vorticity due to rotation). As the tube passes over the ridge, it is squashed so h decreases, and the conservation of potential vorticity stipulates that negative relative vorticity be spun up. This gives rise to anticyclonic curvature in the flow and the tube heads towards the outer wall. Since the fluid is deeper towards the outer wall, the tube gets stretched and soon a positive relative vorticity is spun up. This reverses the flow curvature and eventually the direction, and the tube returns towards the inner wall. As the depth of the fluid decreases, the tube once again gets squashed and a negative relative vorticity is spun up, and the flow changes its course again. As this process is repeated, it creates a meandering flow downstream of the ridge, known as the topographically forced Rossby wave.

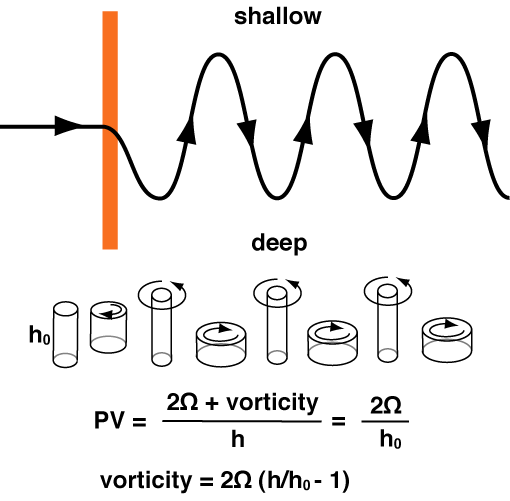The forced Rossby wave is characterized by a stationary phase, with a trough appearing immediately downstream of the topography. A theoretical estimate of the azimuthal wavelength of the stationary Rossby wave is

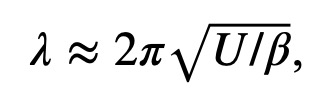where U = r ∆Ω is the azimuthal velocity of the fluid (r : radius, ∆Ω : decrease in the rotation rate of the turntable) and

is the measure of the radial slope of the free surface. Upon substitution,

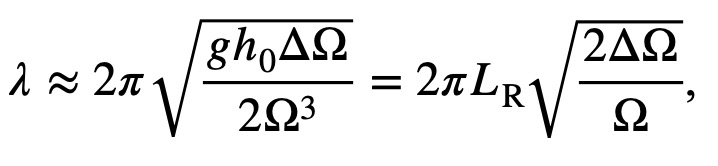where

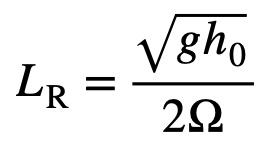is the (external) Rossby radius of deformation. According to the above result, the faster the flow, the greater the wavelength. Notice that in the experiment above, as the flow speed diminishes due to friction, the wavelength does appear to shorten. The wavelength is independent of the shape of the topography. In fact, it is the amplitude, not the scale, of the wave that is affected by the topography. The amplitude of the wave is determined by the projection of the topography on this wave. It turns out that, even though the phase is stationary, the group velocity of the forced Rossby wave points downstream. This explains the downstream excitation of the wave.

There is an important asymmetry in the stationary Rossby wave: it cannot be excited when the flow direction is reversed. In the next experiment, the speed of the turntable is increased from 2.4 to 2.7 rad/sec so the generated flow is retrograde. In this case, no significant meandering pattern emerges downstream of the ridge. The small vorticity anomaly created by the topography quickly moves downstream and dissipated.

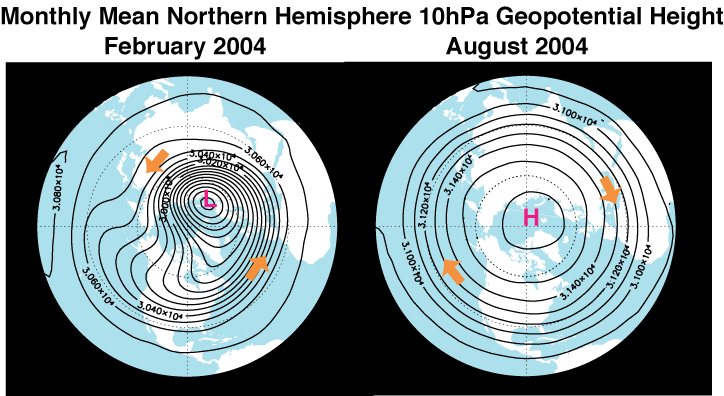
In the atmosphere, stationary Rossby waves are generated by a westerly flow passing over large-scale orography and/or land-sea thermal contrast. The role of the sloped free surface in the experiment is replaced by the latitudinal gradient in the Coriolis parameter, d(2Ω • k)/dy, which is the more common definition of beta. The figure below shows the Northern Hemisphere monthly-mean geopotential height at 10 hPa (~ 30 km) for the months of February and August. At this altitude (middle stratosphere), the zonal winds respond strongly to the seasonality of solar radiation through heating of the ozone layer; they are westerly in winter and easterly in summer. (Geopotential height is, to a good approximation, streamfunction in the extratropics, that is, winds blow parallel to its contours. A westerly flow means that geopotential height decreases toward the pole, whereas an easterly flow means that it increases toward the pole.) The geopotential height field in February is zonally asymmetric, reflecting the stationary Rossby wave propagating into the stratosphere. The predominant zonal wave numbers are one and two, with strong troughs appearing over Eurasia and north America. In August, the geopotential height is much more zonally symmetric, showing that the stationary Rossby wave cannot penetrate into the stratosphere under the easterly condition. This is first predicted theoretically by Charney and Drazin in their seminal paper in 1961.