karman.html

Karman Vortex Street, Mountain Torque (Form Drag), and Eddy-Mean Flow Interaction

In the visible satellite images below, we notice an interesting cloud pattern. In the left picture, the cold, winter monsoon winds blowing out of Siberia cause massive evaporation and formation of convective cloud cells over the East China Sea. (The red arrows indicate the predominant direction of winds.) Notice in the lee of Cheju Island at the tip of the Korean Peninsula there appears a train of vortices in a zigzag pattern, approximately 100km apart from one another. The vortices on the left appear to rotate counterclockwise, whereas those on the right do so clockwise. A similar pattern appears nearby in the lee of Yaku Island south of Kyushu, although it is partially masked by higher clouds to the south. The right picture is yet another example of this type of vortices, this time in the lee side of Guadalupe Island off the lower California. All of these cases involve impingement of an airflow on a tall island mountain: both Cheju and Yaku Islands stand over 1900 m above sea level, and Guadalupe Island above 1250 m. It appears that these vortices are created by an airflow disturbed by the tall island, visualized by low-level clouds atop the marine boundary layer.

These vortices are known as the von Karman vortex street and can be readily reproduced in the laboratory. In the following movie, an isolated "mountain" is seen on the bottom of a rotating tank. The mountain is 3cm in diameter and 2.5cm in height. The depth of the water is about three times the height of the mountain (see the picture below on the right). After the water achieved a counterclockwise solid body rotation at 1.75 radians per second, we inject dye along the circle that intersects with the mountain. Note the camera is rotating with the turntable so that the image appears stationary. At this point the rotation rate of the turntable is increased to 1.80 rps, so the inertia creates a clockwise circulation relative to the tank. Notice how the dye is transformed into a train of vortices in the wake behind the mountain, much like the cloud patterns in the above pictures.

The source of the vortices is the viscous boundary layer on the surface of the mountain. Since the no-slip boundary condition stipulates that the flow velocity vanish at the surface of the mountain, a steady flow around the mountain causes a narrow boundary layer in which velocity has sharp gradients (i.e., vorticity). The sheets of vorticity become unstable in certain parameter range, amplifying in positive and negative signs alternately, shedding vortices in the wake behind the mountain. The vortices tend to be isolated from each other and align themselves in a staggered fasion--the only hydrodynamically stable configuration proved by Theodore von Karman for point vortices in 1911.

It is well kown that the flow geometry around a bluff body is determined by the Reynolds number

where U, L, and v are the flow velocity, the horizontal scale of the object, and the kinematic viscosity coefficient of the fluid, respectively. In the case of a 2D flow around a cylinder, Karman vortices appear when 40 < Re < 200. In the above experiment, U ~ 1.4cm/sec, L ~ 3cm, v ~ 0.01cm²/sec, so Re ~ 420. That this number is higher than the above range is probably because the mountain occupies only a fraction of the fluid column. The cylinder result is based on the experiment in which the cylinder occupies the entire column of fluid. In our case, the flow around the mountain is nearly 2D because of the rotation of the turntable (Taylor-Proudman theorem, see picture below on the left) but the mountain protrudes to only 1/3 of the entire depth. This means that there is less surface area of the viscous boundary layer to generate vorticity. To achieve the flow geometry similar to the standard cylinder case, the mountain must be stretched to fill the entire column; in other words the effect of viscosity needs to be enhanced. Thus we propose an effective Reynolds number

where h and H are the mountain height and the total depth of the water, respectively. In this experiment, h/H ~ 0.3 so Re^* ~ 126, consistent with 40 < Re^*< 200. Note that the rotation of the turntable per se is not essential to the generation of the Karman vorticies. It is simply used as a flow control device.

Mechanisms of flow deceleration. In the above movie, you might have noticed that the shape of the vortices is elongated as they reach further downstream. The deformation of the dye pattern strongly suggests that there is a radial shear in the azimuthal flow in the sense that the flow impinging on the mountain is decelerated relative to the adjacent flow (see picture above on the right). There are two primary mechanisms for this: mountain (pressure) torque (a.k.a. form drag) and eddy-mean flow interaction.

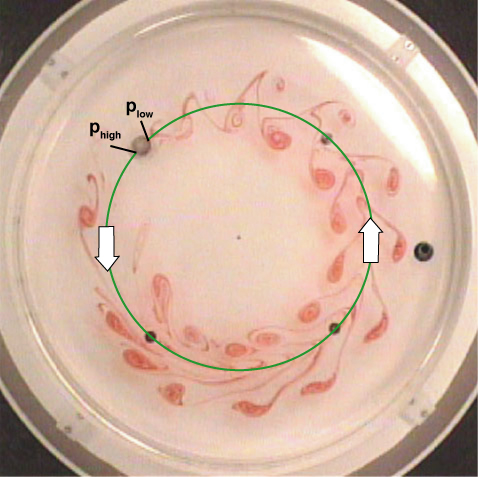Mountain torque (form drag). As the Karman vortices are shed, pressure around the mountain varies with time. On average, however, the upstream pressure is higher than the downstream pressure. This pressure difference is caused by the streamwise asymmetry in the boundary layer structure around the mountain. In the present range of Reynolds number, it is approximately proportional to the square of the mean azimuthal flow velocity. As a result of this pressure difference, the mountain is pushed by the fluid in the downstream direction. In reaction, the mountain pushes back the fluid in the upstream direction. This acts as a drag to the flow. Sometimes the mountain torque is also called pressure torque or form drag.

Eddy-mean flow interaction. In the downstream of the mountains the vortices (eddies) separate into two tracks: cyclonic eddies into the inner track and the anticycronic ones to the outer track. This separation means that there is a net inward transport of vorticity by the eddy. As shown below, this will lead to the deceleration of the azimuthal flow. In the present flow regime, a simple order estimation suggests that the effects of vorticity flux is comparable to that of the mountain torque.

In addition to the mountain torque and eddy-mean flow interaction, the frictional drag at the bottom also decelerates the flow. But this applies uniformly to all fluid elements and does not promote horizontal shear.

where u, v are azimuthal (positive clockwise) and radial (positive outward) velocities, zeta is relative vorticity, R the radial distance from the axis, p_down and p_upare the downstream and upstream pressures at the mountain, rho is density, and F_friction is frictional forces.The overbar and prime denote azimuthal average ("mean") and departure from average ("eddy"), respectively. In the above example, the first term on the right hand side represents mountain torque, and the second term represents the eddy-mean flow interaction. All three terms on the right hand side are negative.